Задача 1
(а) Методом Гаусса-Жордана решить систему линейных уранений 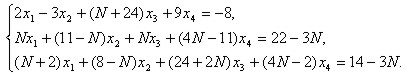
Определить тип системы (совместная/несовместная, определенная/неопределенная), указать размерность многообразия решений.
(б) Заменить все правые части системы на нуль, и для полученной системы линейных однородных уравнений написать общее решение и базис решений.
Задача 2
Используя матричное исчисление, выразить переменные 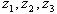 через
через 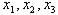 , если:
, если:
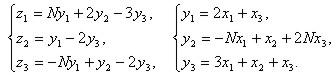
Задача 3
Даны векторы 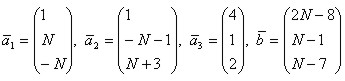 . Показать, что векторы
. Показать, что векторы 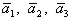 образуют базис в трехмерном пространстве и найти координаты вектора
образуют базис в трехмерном пространстве и найти координаты вектора 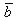 в этом базисе. Соответствующую систему линейных уравнений решить
в этом базисе. Соответствующую систему линейных уравнений решить
а) методом Гаусса - Жордана,
б) матричным методом (методом обратной матрицы),
в) по правилу Крамера.
Задача 4
В балансовой модели Леонтьева с двумя отраслями известны матрица прямых затрат А и вектор конечного продукта b:
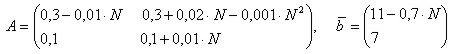
Проверить, что матрица А является продуктивной и вычислить вектор валового выпуска х.
Задача 5
Для треугольной пирамиды с вершинами А(6; 7; N-5), B(10-N; 11; 1), C(8; 9; N-2), D(4-N; 7; -3) найти:
(а) центр масс вершин пирамиды,
(б) длины ребер AB и AD,
(в) угол между ребрами AB и AD,
(г) площадь грани ABC,
(д) объем пирамиды,
(е) угол между ребром AD и гранью ABC.
Задача 6
Прямая L на плоскости имеет уравнение 2х+Ny-2N=0. Дана точка М(-N;1).
(а) Вычислить расстояние от точки М до прямой L.
(б)/(в). Составить уравнение прямой через точку М, параллельную/перпендикулярную прямой L. Выполнить рисунок.
Задача 8
По условию задачи 5 составить:
(ж) уравнения прямой AB,
(з) уравнения высоты (перпендикуляра) через вершину D,
(и) уравнение плоскости треугольника ABC.
Задача 12
Найти пределы функции, не пользуясь правилом Лопиталя.
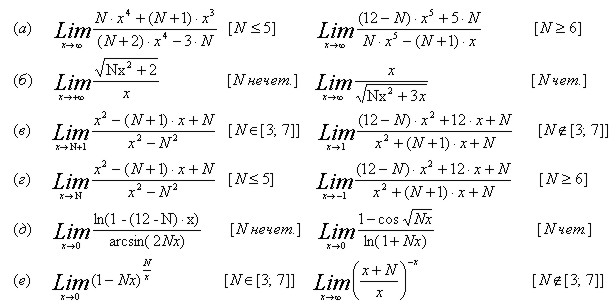
Задача 13
Найти производные 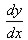 данных функций. Для функций (ж) и (з) найти также
данных функций. Для функций (ж) и (з) найти также 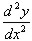
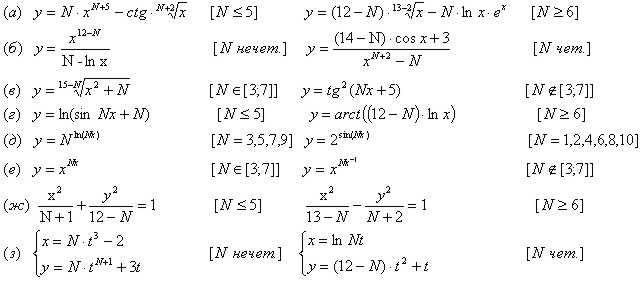
Задача 14
С помощью правила Лопиталя найти пределы.
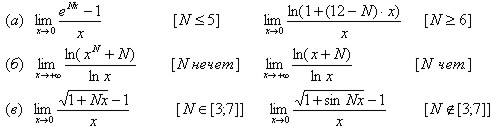
Задача 16
Заготовка ткани имеет форму фигуры на координатной плоскости, ограниченной гиперболами y=N/(N-x), y=N/(N+x) и прямой 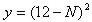 . Требуется выкроить из нее прямоугольник наибольшей площади с одной из сторон, лежащей на данной прямой. Определить площадь прямоугольника. Выполнить рисунок.
. Требуется выкроить из нее прямоугольник наибольшей площади с одной из сторон, лежащей на данной прямой. Определить площадь прямоугольника. Выполнить рисунок.
Задача 17
Дана функция 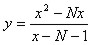 .
.
(а) В точках разрыва функции найти ее пределы слева и справа, а также указать род разрыва.
(б) Найти асимптоты функции.
(в) Исследовать функцию с помощью первой и второй производной, построить граыик функции.
Задача 18
Найти частные производные 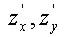 (первого порядка) и
(первого порядка) и 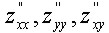 (второго порядка) функции:
(второго порядка) функции:

Задача 20
Предприятие производит два вида товаров. По условиям производства допустимые значения (в некоторых единицах) для годовых объемов х и y выпуска товаров соответственно 1-го и 2-го вида удовлетворяют неравенствам 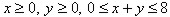 . Функция затрат (в денежных единицах) имеет вид
. Функция затрат (в денежных единицах) имеет вид 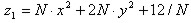 , доход от продаж товаров равен
, доход от продаж товаров равен 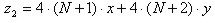 . Прибыль
. Прибыль 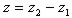
представляет собой разность между доходами и затратами.
(а) Доказать, что z-выпуклая функция от х и y.
(б) Найти оптимальные значения х и y, при которых прибыль z максимальна; вычислить 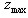 .
.
Задача 38
Вероятность изготовления негодного изделия на некотором предприятии равна 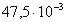 . На предприятии принята упрощённая система контроля качества, вследствии чего часть негодных изделий поступает для реализации и часть годных изделий не поступает для реализации. Вероятность того, что изделие поступит для реализации при условии, что оно годно, равна
. На предприятии принята упрощённая система контроля качества, вследствии чего часть негодных изделий поступает для реализации и часть годных изделий не поступает для реализации. Вероятность того, что изделие поступит для реализации при условии, что оно годно, равна 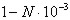 . Вероятность того, что изделие поступит для реализации при условии, что оно негодно, равна
. Вероятность того, что изделие поступит для реализации при условии, что оно негодно, равна 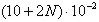 . Найти
. Найти
(а) вероятность того, что изделие является негодным при условии, что оно поступило для реализации,
(б) вероятность того, что изделие является годным при условии, что оно не поступило для реализации.
Задача 39
Рабочий обслуживает три станка. Вероятность того, что в течение смены сломается 1-й, 2-й, 3-й станок, равна 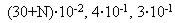 , соответственно, . Найти вероятности следующих событий: в течении смены
, соответственно, . Найти вероятности следующих событий: в течении смены
(а) не сломается ни один станок;
(б) сломается ровно один станок;
(в) сломаются все три станка.
Задача 40
Вероятность обрыва нити на веретене в течение одной минуты равна 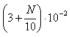 . Прядильная машина управляет работой 100 веретен. С помощью распределения Пуассона найти вероятность того, что за минуту
. Прядильная машина управляет работой 100 веретен. С помощью распределения Пуассона найти вероятность того, что за минуту
(а) произойдут обрывы на 3 веретенах;
(б) количество веретен, на которых произойдут обрывы, не будет превосходить 3.
Задача 41
В таблице представлен статистический ряд выборки дискретной случайной величины X.
Вычислить выборочное среднее, выборочную дисперсию (простую и улучшенную - т. наз. "несмещенную"), выборочное среднее квадратичное отклонение случайной величины Х.
Задача 42
Непрерывная случайная величина Х со значениями на отрезке -N<x<N имеет плотность распределения вероятностей 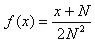 . Найти функцию распределения F(X), математическое ожидание (среднее значение) М(X), дисперсию D(X), среднее квадратичное отклонение
. Найти функцию распределения F(X), математическое ожидание (среднее значение) М(X), дисперсию D(X), среднее квадратичное отклонение 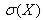 , вероятность
, вероятность 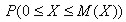 , квантиль
, квантиль 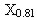 уровня значимости 0,81 случайной величины X. (При 0<p<1 квантиль
уровня значимости 0,81 случайной величины X. (При 0<p<1 квантиль 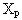 определяется уравнением
определяется уравнением 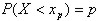 , или
, или 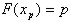 ).
).
Задача 45
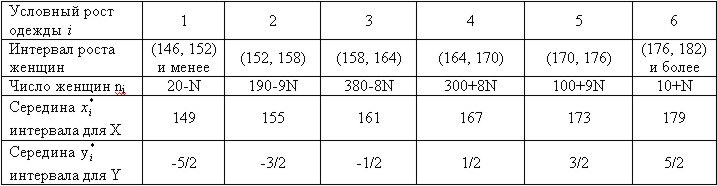
(а) Для роста женщин найти выборочное среднее и выборочное среднее квадратичное отклонение.
(б) Предполагается, что рост женщин в хорошем приближении подчиняется нормальному распределению. Рассчитать ассортимент дамских пальто в % по условному росту одежды для швейной фабрики, изготовляющей женскую одежду для данной местности.
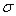 мм. Найти:
мм. Найти: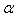 мм и меньше
мм и меньше 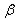 мм;
мм;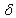 мм.
мм.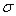 ,
, 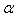 ,
, 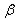 ,
, 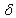 даны.
даны.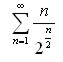
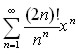 .
.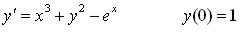 .
.Найти интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости:
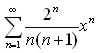 .
. 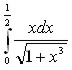
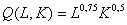 .
.
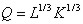 . Найдите функцию общих затрат, а затем, из условия максимизации прибыли – функцию предложения по цене, если rL=p3, rK=p1.
. Найдите функцию общих затрат, а затем, из условия максимизации прибыли – функцию предложения по цене, если rL=p3, rK=p1.
Найти функцию спроса
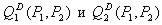 для индивида, если его функция полезности имеет вид:
для индивида, если его функция полезности имеет вид: 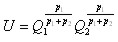 , а бюджет ограничен М денежными единицами.
, а бюджет ограничен М денежными единицами.
Для функции полезности
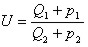 получить аналитические выражения для функции спроса на благо
получить аналитические выражения для функции спроса на благо 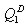 , рассчитать коэффициент прямой эластичности спроса по цене E1Q1 и коэффициент перекрёстной эластичности спроса по цене E2Q2. Считать, что бюджет ограничен М денежными единицами.
, рассчитать коэффициент прямой эластичности спроса по цене E1Q1 и коэффициент перекрёстной эластичности спроса по цене E2Q2. Считать, что бюджет ограничен М денежными единицами.